Who needs gradient descent? Getting to grips with Nevergrad.

February 21, 2021

Introduction

Nevergrad is an interesting and quite wonderful Python library that I’ve grown fond of over the last few months. It provides tooling to run numerical optimization without having to rely on computing the gradient of the function you’re optimizing (in stark contrast to the current algorithm du jour of the deep learning world, gradient descent). Think evolutionary algorithms, particle swarm optimization and so on.

I like a few things about nevergrad, and it’s since become my go-to tool for ad-hoc optimization problems, mostly due to how easy it has been to drop into my code. So, today, I’d like to talk about nevergrad for a bit.

What I really like about Nevergrad

My appreciation for nevergrad boils down to two things:

Easy of use
Flexibility

As you’ll see in the example latter on, nevergrad is surprisingly quick to integrate into your existing code. From an end-user’s point of view, it’s almost impossible to overstate how important it is to minimize the time between “zero” and “Hello world!". To begin optimizing with nevergrad, it takes only a couple lines of code. I love this aspect. This emphasis on designing the API so that you can be productive immediately is something I increasingly appreciate in software that chooses to optimize developer productivity. Full marks.

Despite this, nevergrad is also relatively flexible. Utilizing “gradient-free” optimization means you don’t need to worry about having your code be differentiable by some opaque backend. This allows you to wrap any function you wish, with no additional modification required on your part. As long as you output some kind of computed loss that you want minimized, you can use nevergrad. No matter the control flow. This makes it especially handy when you’re trying to figure out hyperparameters for a certain process – you don’t need to modify your code to make it compatible. Just wrap nevergrad around it and away you go. For example, I once wrapped a process that involved training an ML model, followed by running an ODE numerical solver, before finally calculating a set of metrics, each with their own set of tunable parameters. I was able to find a close-to-optimal solution using nevergrad without having to modify any of the process code.

A basic example

As always, an example is (usually) best. Imagine you want to find the minimum point of the following parabola:

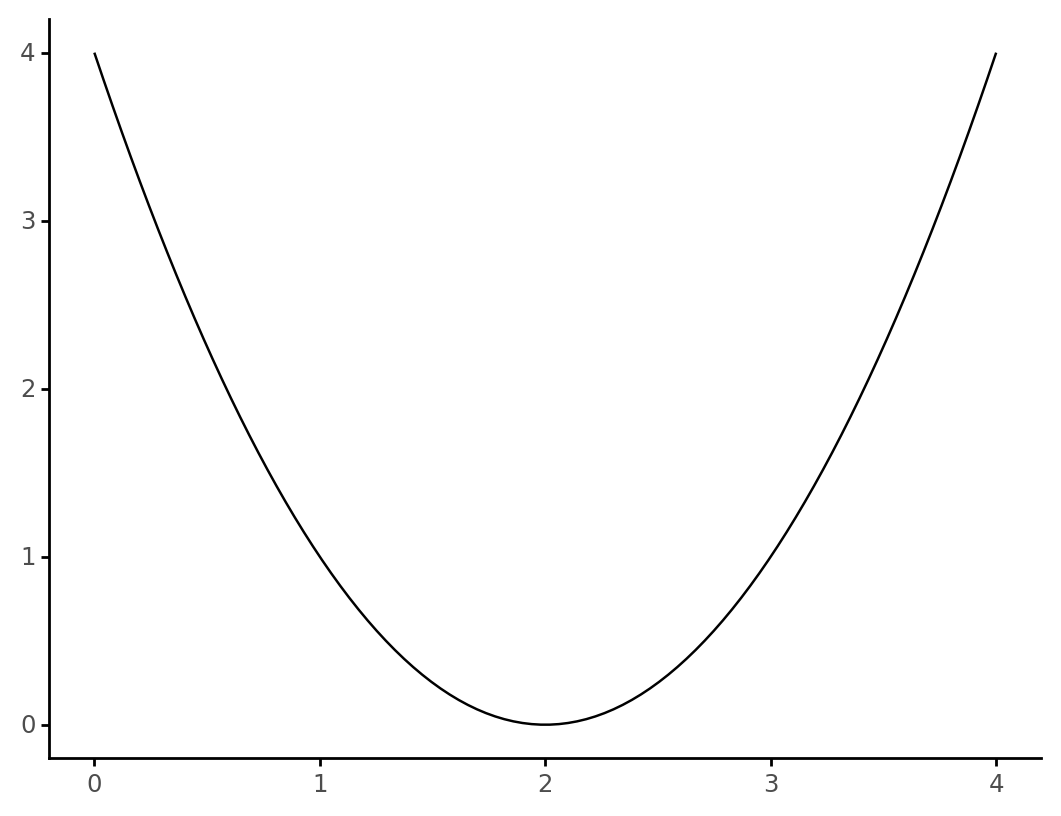
which has the following expression: $$ y = (x - 2)^2. $$

With nevergrad, all we need to do is this:

import nevergrad as ng

def square_function(x):
    return (x-2)**2

x_arg = ng.p.Scalar()  # Define our argument to the function
instru = ng.p.Instrumentation(x_arg)  # Package it as "instrumentation"

optimizer = ng.optimizers.OnePlusOne(parametrization=instru, budget=100)  # Choose an optimizer, passing through our instrumentation
recommendation = optimizer.minimize(square_function)  # Find the minima!
print(recommendation.value)

# >>> ((1.9998271159560648,), {})

In other words,

Define our function.
Define our input arguments to the function This happens to be the explicit way of defining our instrumentation. There is convenient short-hand as well. (there are lots to choose from, including integer values and choices!)
Choose our optimization algorithm.
Optimize.

Nice!

A more practical example: hyperparameter optimization

A more practical example (and one where I originally discovered the value of nevergrad) is for hyperparameter optimization.

While working on my PhD I encountered the following problem. I wanted to predict a smooth curve (that I had measured) by adding together a number of scaled smooth kernels. And I would scale the kernels according to some input data.

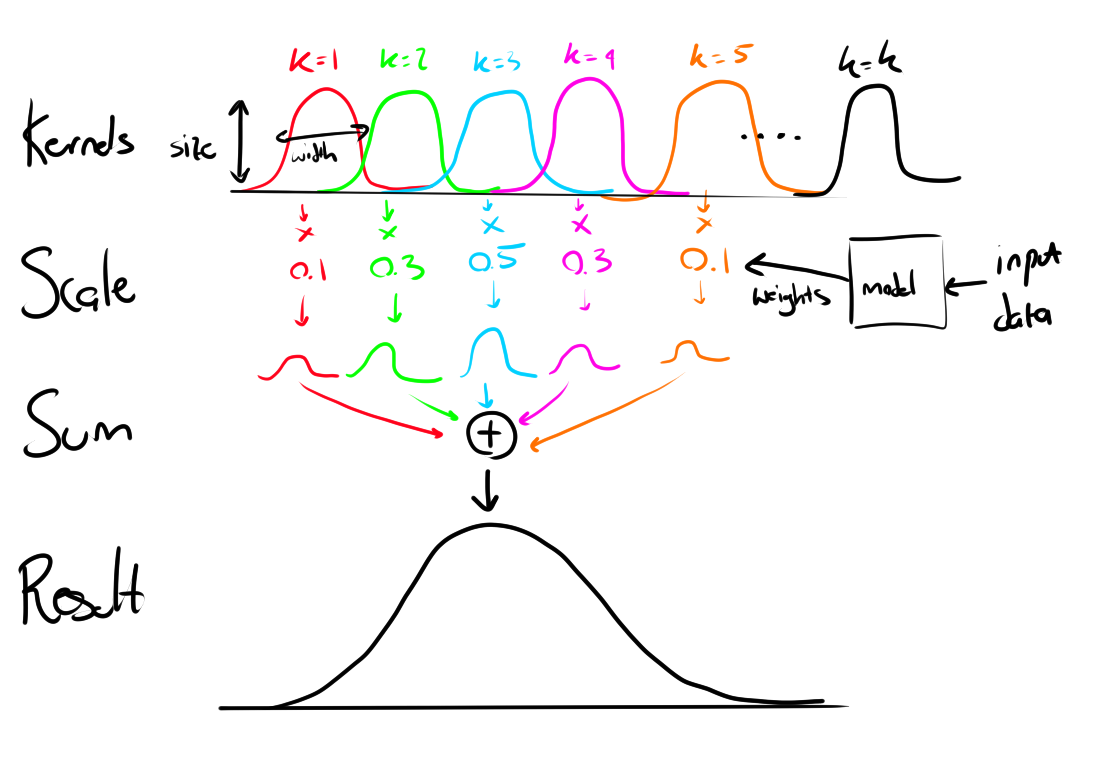
So, the general process was “scale” each of the kernels according to data, then add them together to create the final smooth curve. The code looks something like this:

X, y = create_training_data(samples)
X = make_features(X_train)

kernels = make_kernels(num_kernels, size, width)

model = train_model(X, y, kernels)
y_hat = model.predict(X)
score = mean_squared_error(y, y_hat)

The model would give me the weights of each kernel, but:

How many kernels should there be?
What size should each kernel start as?
What width should each kernel be?

Choosing the right (or wrong) values for the above parameters (number of kernels, their size and their width) would dramatically effect the accuracy of the final smooth curve.

I could try every possible combination of values, and choose the one that works the best, but this is an incredibly time consuming process. I have thousands of these smooth curves I want to predict, and training the model takes too long to make this an attractive option. So let’s use nevergrad to find a optimal set of hyperparameters instead.

First, we need to wrap our above code in a function that we can optimize over:

def calculate_model_score(num_kernels, size, width):
    X, y = create_training_data(samples)
    X = make_features(X_train)

    kernels = make_kernels(num_kernels, size, width)

    model = train_model(X, y, kernels)
    y_hat = model.predict(X)
    score = mean_squared_error(y, y_hat)

And do our instrumentation and optimization as before: Notice here that we also further customize our instrumentation by setting upper and lower limits, and make sure the number of kernels is an integer.

num_kernels = ng.p.Scalar(lower=10, upper=60).set_integer_casting()
size = ng.p.Scalar(lower=0.001, upper=10)
shape = ng.p.Scalar(lower=0.0001, upper=0.01)

instru = ng.p.Instrumentation(num_kernels, size, shape)
optimizer = ng.optimizers.OnePlusPne(parametrization=instru, budget=300)
recommendation=optimizer.minimize(calculate_model_score)
print(recommendation.value[0])
# >>> (53, 1.8828894598055905, 0.004852569379631386)

And there we have it, 53 kernels with a size of 1.882 and width of 0.0048 gives us our best result. Note:

We didn’t have to modify any of the logic in our code (just wrap it in a self-containing function)
We had to add ~7 independent lines of code (less, if you want to be more terse).

It’s refreshing to have a tool this useful integrate so easily and seamlessly into your existing code, and this is often why I find myself reaching for nevergrad instead of refactoring code to work with something else, like jax. Sometimes some quick-and-dirty optimization using an evolutionary algorithm can be good enough (not to mention fast). Sure, this particular example isn’t the ideal candidate for gradient descent, but refactoring so that these kernel parameters become model parameters, and then optimizing using jax and gradient descent is something that I’ve done before. It worked too – but it took a lot longer than simply plugging in nevergrad.

Oh, I’m we’re barely scratching the surface of what nevergrad can do, particularly when interacting with ML workflows.

Closing thoughts

And that’s nevergrad, the optimization library that doesn’t use gradient descent. It’s easy to use (and easy to integrate), very flexible and has a decent API. I happen to like it a fair deal, and expect to use it more frequently in the future. If it sounds like something you’re interested, I can highly recommend it. Check out the documentation, if you want to read more.

Till next time,
Michael.